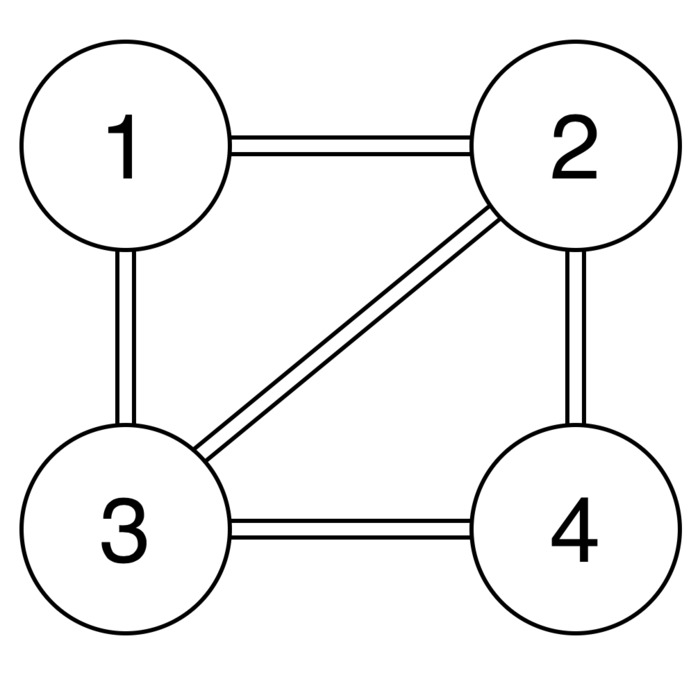
Hi there! Today’s program aims to solve the minimum cut problem. It is another one that I learned in Algorithms: Design and Analysis, Part 1 course from Coursera. A cut is partition of a graph and partitioning a graph means dividing it into two disjoint subsets of vertices. The minimum cut then would be such that the number of edges going from one partition to the other is minimal. Below is a simple example of a graph with 4 nodes. There are two minimum cuts for it, namely cutting the node 1 or 4 out. Each one of these cuts has 2 edges going across the partitions. The goal of my program is to show what this number of edges is, not caring what the exact number of minimum cuts is.
The algorithm implemented is called Random Contraction Algorithm. It was invented by Karger in the early 1990s. As the name implies, it has some randomness in it. The basics of it are simple: given a graph, choose an edge and contract its vertices into one. Do this until there are only two nodes left. This may or may not give the minimum cut, so it has to be run multiple times to actually give the minimum cut with high probability. I implemented a loop that calls this algorithm and saves the number of crossing edges in the minimum cut so far. It is presented below.
package main
import (
"bufio"
"bytes"
"encoding/gob"
"fmt"
"log"
"math"
"os"
"strconv"
"strings"
"time"
)
func randomContraction(
nodes map[int]*Node,
maxNode int) int {
for len(nodes) > 2 {
start := 0
end := 0
// get two keys at random
findingEdge:
for s, node := range nodes {
for e, _ := range node.Edges {
start = s
end = e
break findingEdge
}
}
maxNode++
nodes[maxNode] = &Node{
Id: maxNode,
Edges: make(map[int]int)}
for e, v := range nodes[start].Edges {
if e != end {
nodes[maxNode].Edges[e] += v
nodes[e].Edges[maxNode] += nodes[e].Edges[start]
delete(nodes[e].Edges, start)
}
}
for e, v := range nodes[end].Edges {
if e != start {
nodes[maxNode].Edges[e] += v
nodes[e].Edges[maxNode] += nodes[e].Edges[end]
delete(nodes[e].Edges, end)
}
}
delete(nodes, start)
delete(nodes, end)
}
smallestCut := maxNode * 100
for _, v := range nodes {
thisCut := 0
for _, weight := range v.Edges {
thisCut += weight
}
if thisCut < smallestCut {
smallestCut = thisCut
}
}
return smallestCut
}
type Node struct {
Id int // beginning of vertex
Edges map[int]int // end -> weight
}
func main() {
start := time.Now()
N := 0
fmt.Scanf("%d", &N)
nodes := make(map[int]*Node)
fmt.Printf("N = %d\n", N)
maxNode := 0
in := bufio.NewReaderSize(os.Stdin, 2000)
for i := 0; i <= N; i++ {
aux := 0
input, err := in.ReadString('\n')
if err != nil {
break
}
numbers := strings.Fields(input)
if len(numbers) <= 0 {
continue
}
aux, _ = strconv.Atoi(numbers[0])
if aux > maxNode {
maxNode = aux
}
if nodes[aux] == nil {
nodes[aux] = &Node{
Id: aux,
Edges: make(map[int]int)}
}
currentNode := nodes[aux]
for k := 1; k < len(numbers); k++ {
aux, _ = strconv.Atoi(numbers[k])
if nodes[aux] == nil {
// create end vertex if not existent
nodes[aux] = &Node{
Id: aux,
Edges: make(map[int]int)}
}
currentNode.Edges[aux] += 1
}
}
smallestCut := N
//encoding
var mod bytes.Buffer
enc := gob.NewEncoder(&mod)
dec := gob.NewDecoder(&mod)
iterations := int(
float64(N*N) * math.Log(float64(N)))
for i := 1; i <= iterations; i++ {
err := enc.Encode(nodes)
if err != nil {
log.Fatal("encode error:", err)
}
nodesToContract := make(map[int]*Node)
err = dec.Decode(&nodesToContract)
if err != nil {
log.Fatal("decode error:", err)
}
cut := randomContraction(
nodesToContract, maxNode)
if cut < smallestCut {
smallestCut = cut
fmt.Printf("New smallest cut: %d\n",
smallestCut)
}
if i%200 == 0 {
fmt.Printf("Current iteration: %d\n", i)
}
}
fmt.Printf("Smallest Cut after contraction: %d\n",
smallestCut)
elapsed := time.Since(start)
fmt.Printf("Total iterations: %d\n",
iterations)
fmt.Printf("Random contractions took %s\n",
elapsed)
}
The biggest challenge was reading the input file correctly. This happened because I was not used at reading this in Go. Firstly, I tried to read the input file and use sprintf to analyse each line, but I couldn’t find a solution to read an unknown number of variables in the strings.
The file has the total number of nodes in the first line and then the other lines have information about the connections for each node. The input file below is the same as the picture presented in the beginning of this post.
4
1 2 3 # indicates node 1 is connected to nodes 2 and 3
2 1 3 4
3 1 2 4
4 2 3
The output for this case is
N = 4
New smallest cut: 3
New smallest cut: 2
Smallest Cut after contraction: 2
Total iterations: 22
Random contractions took 883.278µs
With a little tweaking, it can also show what are the edges in each partition. Here is an implementation that adds sets of vertices to it. In the end, it is just needed to print the numbers in the sets of the two nodes remaining. At this time, I couldn’t find a native implementation of sets in Go. The one in the example was based on this with my own additions.
That’s all for this post! Thanks for reading!